数学竞赛知识点资料思维导图
凉笙微凉
2023-04-04

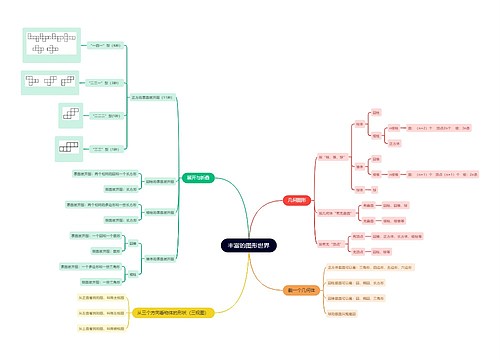
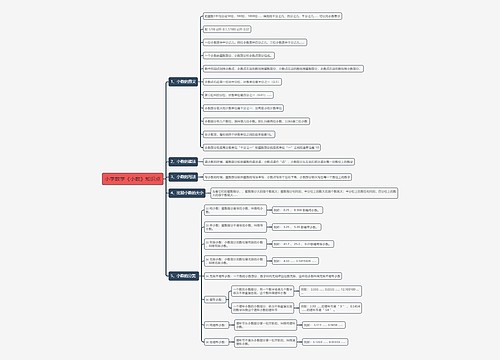
模板展示了数学竞赛的知识点,包含初中数学联赛竞赛知识点和计算知识点归纳两部分内容,在初中数学联赛竞赛知识点部分,包含了平行四边形的性质和判定、对称性内容,而在计算知识点归纳部分,介绍了鸡兔同笼问题的基本概念、思路和公式,并对一些常见的计算题目进行了详细的解释和归纳,数学竞赛知识点资料思维导图希望这些资料能对大家的学习有所帮助。
思维导图大纲
相关思维导图模版
数学竞赛获奖感言范文(优选15篇)思维导图
 蓝胖子
蓝胖子树图思维导图提供《数学竞赛获奖感言范文(优选15篇)》在线思维导图免费制作,点击“编辑”按钮,可对《数学竞赛获奖感言范文(优选15篇)》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:36a99bb8b7c3a9264f4a2258cd78b34e
数学课程学期教学计划思维导图
 西风不相识
西风不相识树图思维导图提供《数学课程学期教学计划》在线思维导图免费制作,点击“编辑”按钮,可对《数学课程学期教学计划》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:f80b4672f11401ab2b26771fb770a969