2022高考数学解题技巧思维导图
清风浅
2023-04-04

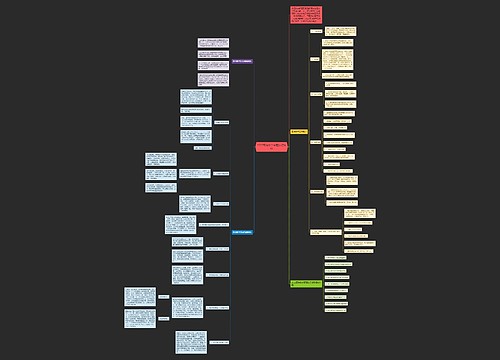
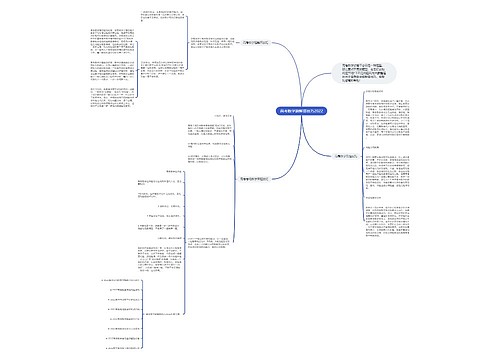
2022高考数学解题技巧思维导图面对数学题,考生可以运用一些有效的技巧来提高答题效率,在答小题和填空题时,可以使用简单的方法蒙答案,而对于大题,则可以将题干中的关键词用笔画出来,更直观地解题,考生还可以采用充分联想回忆基本知识和题型、全方位、多角度分析题意、恰当构造辅助元素解题技巧来解决数学难题。而在具体解题过程中,对绝对值问题、因式分解、配方法和换元法掌握技巧也是至关重要的,掌握这些解题技巧,相信每位考生都能在2022高考数学中表现出色。
思维导图大纲
相关思维导图模版
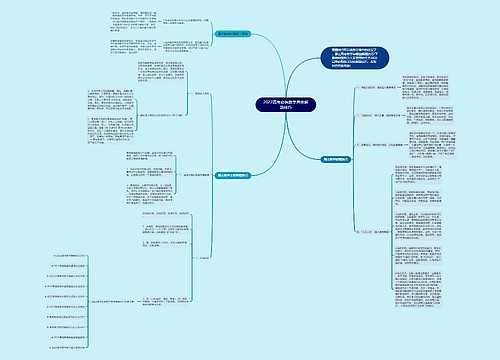
2022高考实用的数学解题小技巧思维导图
 琴瑟如你
琴瑟如你树图思维导图提供《2022高考实用的数学解题小技巧》在线思维导图免费制作,点击“编辑”按钮,可对《2022高考实用的数学解题小技巧》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:61b832843e5ab7e9f20f412a12654ecd
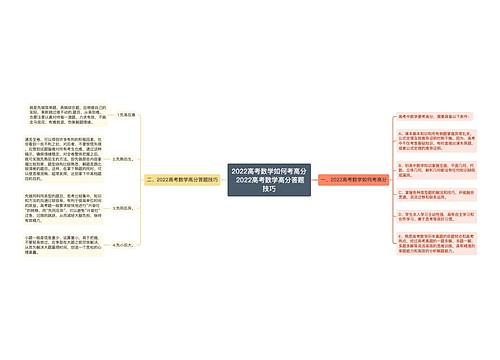
2022高考数学如何考高分 2022高考数学高分答题技巧思维导图
 心不动则不痛
心不动则不痛树图思维导图提供《2022高考数学如何考高分 2022高考数学高分答题技巧》在线思维导图免费制作,点击“编辑”按钮,可对《2022高考数学如何考高分 2022高考数学高分答题技巧》进行在线思维导图编辑,本思维导图属于思维导图模板主题,文件编号是:161a1190fa3a595513e5fc7042a51c8c