高考数学高分必须掌握的技巧思维导图

不爱计较

2023-04-04

浏览量: 1

高考数学高分技巧

高考数学技巧

高考

数学

技巧

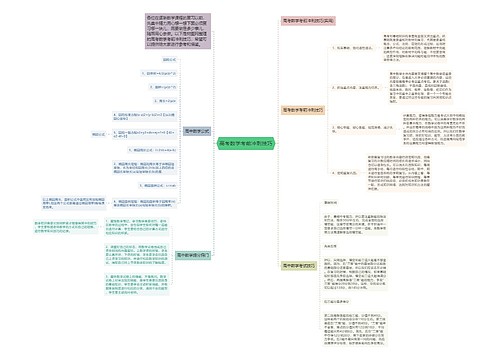
高考数学高分必须掌握的技巧思维导图，包含解题顺序技巧和高分答题技巧，解题顺序上，应该先做熟练掌握的题目，先同科同类型的题目，先小后大，先点后面，先高后低，高分答题技巧上，通览全卷是重要的方法，特别是解答那些一眼看得出结论的简单选择或填空题。在做其他难一些的题目时，可以将其分为熟悉的和陌生的两类，从易到难，稳步前进，还应注意掌握每道题所占分值，对不同类型题材有所了解，这些技巧和思路可以帮助考生冷静应对高考数学，取得更好成绩。

思维导图大纲

高考数学拿高分的技巧

数学答题顺序技巧——先熟后生

通览全卷，可以得到许多有利的积极因素，也会看到一些不利之处，对后者，不要惊慌失措，应想到试题偏难对所有考生也难，通过这种暗示，确保情绪稳定，对全卷整体把握之后，就可实施先熟后生的策略，即先做那些内容掌握比较到家、题型结构比较熟悉、解题思路比较清晰的题目。这样，在拿下熟题的同时，可以使思维流畅、超常发挥，达到拿下中高档题目的目的。

数学答题顺序技巧——先同后异

先做同科同类型的题目，思考比较集中，知识和方法的沟通比较容易，有利于提高单位时间的效益。高考题一般要求较快地进行"兴奋灶"的转移，而"先同后异"，可以避免"兴奋灶"过急、过频的跳跃，从而减轻大脑负担，保持有效精力，

数学答题顺序技巧——先小后大

小题一般是信息量少、运算量小，易于把握，不要轻易放过，应争取在大题之前尽快解决，从而为解决大题赢得时间，创造一个宽松的心理基矗

数学答题顺序技巧——先点后面

近年的高考数学解答题多呈现为多问渐难式的"梯度题"，解答时不必一气审到底，应走一步解决一步，而前面问题的解决又为后面问题准备了思维基础和解题条件，所以要步步为营，由点到面

数学答题顺序技巧——先高后低

即在考试的后半段时间，要注重时间效益，如估计两题都会做，则先做高分题;估计两题都不易，则先就高分题实施"分段得分"，以增加在时间不足前提下的得分。

高考数学高分答题技巧

高考数学高分答题技巧之通览全卷

1.解答那些一眼看得出结论的简单选择或填空题(一旦解出，情绪会立即稳定).

2.其他不能立即作答的题目，可一边通览，一边粗略分为a、b两类:a类指题型比较熟悉、预计上手比较容易的题目;b类是题型比较陌生、自我感觉比较困难的题目.

3.做到三个心中有数:对全卷一共有几道大小题有数，防止漏做题，对每道题各占几分心中有数，大致区分一下哪些属于代数题，哪些属于三角题，哪些属于综合型的题.

通览全卷是克服"前面难题做不出，后面易题没时间做"的有效措施，也从根本上防止了"漏做题".对于同一道题目，有的人理解的深，有的人理解的浅，有的人解决的多，有的人解决的少.为了区分这种情况，高考的阅卷评分办法是懂多少知识就给多少分.这种方法我们叫它"分段评分"，或者"踩点给分"--踩上知识点就得分，踩得多就多得分.

高考数学高分答题技巧之答题顺序

先易后难

就是先做简单题，再做综合题，应根据自己的实际，果断跳过啃不动的题目，从易到难，也要注意认真对待每一道题，力求有效，不能走马观花，有难就退，伤害解题情绪。

高考数学的答题顺序：先小后大

小题一般是信息量少、运算量小，易于把握，不要轻易放过，应争取在大题之前尽快解决，从而为解决大题赢得时间，创造一个宽松的心理基矗

先点后面

近年的高考数学解答题多呈现为多问渐难式的"梯度题"，解答时不必一气审到底，应走一步解决一步，而前面问题的解决又为后面问题准备了思维基础和解题条件，所以要步步为营，由点到面6.先高后低。即在考试的后半段时间，要注重时间效益，如估计两题都会做，则先做高分题;估计两题都不易，则先就高分题实施"分段得分"，以增加在时间不足前提下的得分。

高考数学高分答题技巧之分段得分

"分段得分"的基本精神是，会做的题目力求不失分，部分理解的题目力争多得分.

1.对于会做的题目，要解决"会而不对，对而不全"这个老大难问题.有的考生拿到题目，明明会做，但最终答案却是错的--会而不对.有的考生答案虽然对，但中间有逻辑缺陷或概念错误，或缺少关键步骤--对而不全.因此，会做的题目要特别注意表达的准确、考虑的周密、书写的规范、语言的科学，防止被"分段扣点分".经验表明，对于考生会做的题目，阅卷老师则更注意找其中的合理成分，分段给点分，所以"做不出来的题目得一二分易，做得出来的题目得满分难".

2.对绝大多数考生来说，更为重要的是如何从拿不下来的题目中分段得点分.我们说，有什么样的解题策略，就有什么样的得分策略.把你解题的真实过程原原本本写出来，就是"分段得分"的全部秘密.

(1)缺步解答.如果遇到一个很困难的.问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败.特别是那些解题层次明显的题目，或者是已经程序化了的方法，每一步得分点的演算都可以得分.

(2)跳步答题.解题过程卡在某一过渡环节上是常见的.这时，我们可以先承认中间结论，往后推，看能否得到结论.如果不能，说明这个途径不对，立即改变方向;如果能得出预期结论，就回过头来，集中力量攻克这一"卡壳处".由于考试时间的限制，"卡壳处"的攻克如果来不及了，就可以把前面的写下来，再写出"证实某步之后，继续有……"一直做到底.也许，后来中间步骤又想出来，这时不要乱七八糟插上去，可补在后面.若题目有两问，第一问想不出来，可把第一问作"已知"，"先做第二问"，这也是跳步解答.

(3)退步解答."以退求进"是一个重要的解题策略.如果你不能解决所提出的问题，那么，你可以从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从较强的结论退到较弱的结论.总之，退到一个你能够解决的问题.为了不产生"以偏概全"的误解，应开门见山写上"本题分几种情况".这样，还会为寻找正确的、一般性的解法提供有意义的启发.

(4)辅助解答.一道题目的完整解答，既有主要的实质性的步骤，也有次要的辅助性的步骤.实质性的步骤未找到之前，找辅助性的步骤是明智之举.如:准确作图，把题目中的条件翻译成数学表达式，设应用题的未知数等.答卷中要做到稳扎稳打，字字有据，步步准确，尽量一次成功，提高成功率.试题做完后要认真做好解后检查，看是否有空题，答卷是否准确，所写字母与题中图形上的是否一致，格式是否规范，尤其是要审查字母、符号是否抄错，在确信万无一失后方可交卷.

高考数学应考的技巧

一、提前进入"角色"

高考前一个晚上睡足八个小时，早晨吃好清淡早餐，按清单带齐一切用具，提前半小时到达考区，一方面可以消除紧张、稳定情绪、从容进场，另一方面也留有时间提前进入"角色"——让大脑开始简单的数学活动，进入单一的数学情境。如：

1.清点一下用具是否带齐(笔、橡皮、作图工具、身分证、准考证等)。

2.把一些基本数据、常用公式、重要定理在脑子里"过过电影"。

3.最后看一眼难记易忘的知识点。

4.互问互答一些不太复杂的问题。

二、精神要放松，情绪要自控

最易导致紧张、焦虑和恐惧心理的是入场后与答卷前的"临战"阶段，此时保持心态平衡的方法有三种：①转移注意法：避开临考者的目光，把注意力转移到某一次你印象较深的数学模拟考试的评讲课上，或转移到对往日有趣、滑稽事情的回忆中。②自我安慰法：如"我经过的考试多了，没什么了不起"，"考试，老师监督下的独立作业，无非是换一换环境"等。③抑制思维法：闭目而坐，气贯丹田，四肢放松，深呼吸，慢吐气，(最好默念几遍："阿弥陀佛"呵呵，还真的管用)如此进行到发卷时。

三、迅速摸透"题情"

刚拿到试卷，一般心情比较紧张，不忙匆匆作答，可先从头到尾、正面反面通览全卷，尽量从卷面上获取最多的信息，为实施正确的解题策略作全面调查，一般可在十分钟之内做完三件事：

1.顺利解答那些一眼看得出结论的简单选择或填空题(一旦解出，情绪立即会稳定)。

2.对不能立即作答的题目，可一面通览，一面粗略分为A、B两类：A类指题型比较熟悉、估计上手比较容易的题目，B类是题型比较陌生、自我感觉比较困难的题目。

3.做到三个心中有数：对全卷一共有几道大小题有数，防止漏做题，对每道题各占几分心中有数，大致区分一下哪些属于代数题，哪些属于三角题，哪些属于综合型的题。

通览全卷是克服"前面难题做不出，后面易题没时间做"的有效措施，也从根本上防止了"漏做题"。

四、信心要充足，暗示靠自己

答卷中，见到简单题，要细心，莫忘乎所以，谨防"大意失荆州"。面对偏难的题，要耐心，不能急。考试全程都要确定"人家会的我也会，人家不会的我也会"的必胜信念，使自己始终处于最佳竞技状态。

五、三先三后

在通览全卷、并作了简单题的第一遍解答后，情绪基本趋于稳定，大脑趋于亢奋，此后七八十分钟内就是最佳状态的发挥或收获丰硕果实的黄金季节了。实践证明，满分卷是极少数，绝大部分考生都只能拿下部分题目或题目的部分得分。因此，实施"三先三后"及"分段得分"的考试艺术是明智的。

1.先易后难。就是说，先做简单题，再做复杂题;先做A类题，再做B类题。当进行第二遍解答时(通览并顺手解答算第一遍)，就无需拘泥于从前到后的顺序，应根据自己的实际，跳过啃不动的题目，从易到难。

2.先高(分)后低(分)。这里主要是指在考试的`后半段时要特别注重时间效益，如两道题都会做，先做高分题，后做低分题，以使时间不足时少失分;到了最后十分钟，也应对那些拿不下来的题目就高分题"分段得分"，以增加在时间不足前提下的得分。

3.先同后异。就是说，可考虑先做同学科同类型的题目。这样思考比较集中，知识或方法的沟通比较容易，有利于提高单位时间的效益。一般说来，考试解题必须进行"兴奋灶"的转移，思考必须进行代数学科与几何学科的相互换位，必须进行从这一章节到那一章节的跳跃，但"先同后异"可以避免"兴奋灶"过急、过频和过陡的跳跃。

三先三后，要结合实际，要因人而异，谨防"高分题久攻不下，低分题无暇顾及"。

六、一慢一快

就是说，审题要慢，做题要快。

题目本身是"怎样解这道题"的信息源，所以审题一定要逐字逐句看清楚，力求从语法结构、逻辑关系、数学含义等各方面真正看清题意。解题实践表明，条件预示可知并启发解题手段，结论预告需知并诱导解题方向。凡是题目未明显写出的，一定是隐蔽给予的，只有细致的审题才能从题目本身获得尽可能多的信息，这一步不要怕慢。

找到解题方法后，书写要简明扼要，快速规范，不要拖泥带水，啰嗦重复，尤忌画蛇添足。一般来说，一个原理写一步就可以了，至于不是题目考查的过渡知识，可以直接写出结论。高考允许合理省略非关键步骤。

为了提高书写效率，应尽量使用数学语言、符号，这比文字叙述要节省而严谨。

七、分段得分

对于同一道题目，有的人理解得深，有的人理解得浅，有的人解决得多，有的人解决得少。为了区分这种情况，高考的阅卷评分办法是懂多少知识就给多少分。这种方法我们叫它"分段评分"，或者"踩点给分"——踩上知识点就得分，踩得多就多得分。

鉴于这一情况，高考中对于难度较大的题目采用"分段得分"的策略实为一种高招儿。其实，考生的"分段得分"是高考"分段评分"的逻辑必然。"分段得分"的基本精神是，会做的题目力求不失分，部分理解的题目力争多得分。

1.对于会做的题目，要解决"会而不对，对而不全"这个老大难问题。有的考生拿到题目，明明会做，但最终答案却是错的——会而不对。有的考生答案虽然对，但中间有逻辑缺陷或概念错误，或缺少关键步骤——对而不全。因此，会做的题目要特别注意表达的准确、考虑的周密、书写的规范、语言的科学，防止被"分段扣点分"。经验表明，对于考生会做的题目，阅卷老师则更注意找其中的合理成分，分段给点分，所以"做不出来的题目得一二分易，做得出来的题目得满分难"。

2.对绝大多数考生来说，更为重要的是如何从拿不下来的题目中分段得点分。我们说，有什么样的解题策略，就有什么样的得分策略。把你解题的真实过程原原本本写出来，就是"分段得分"的全部秘密。

①缺步解答

如果遇到一个很困难的问题，确实啃不动，一个聪明的解题策略是，将它们分解为一系列的步骤，或者是一个个小问题，先解决问题的一部分，能解决多少就解决多少，能演算几步就写几步，尚未成功不等于失败。特别是那些解题层次明显的题目，或者是已经程序化了的方法，每进行一步得分点的演算都可以得分，最后结论虽然未得出，但分数却已过半，这叫"大题拿小分"，确实是个好主意。

②跳步答题

解题过程卡在某一过渡环节上是常见的。这时，我们可以先承认中间结论，往后推，看能否得到结论。如果不能，说明这个途径不对，立即改变方向;如果能得出预期结论，就回过头来，集中力量攻克这一"卡壳处"。

由于考试时间的限制，"卡壳处"的攻克来不及了，那么可以把前面的写下来，再写出"证实某步之后，继续有……"一直做到底，这就是跳步解答。

也许，后来中间步骤又想出来，这时不要乱七八糟插上去，可补在后面，"事实上，某步可证明或演算如下"，以保持卷面的工整。若题目有两问，第一问想不出来，可把第一问作"已知"，"先做第二问"，这也是跳步解答。

③退步解答

"以退求进"是一个重要的解题策略。如果你不能解决所提出的问题，那么，你可以从一般退到特殊，从抽象退到具体，从复杂退到简单，从整体退到部分，从较强的结论退到较弱的结论。总之，退到一个你能够解决的问题。为了不产生"以偏概全"的误解，应开门见山写上"本题分几种情况"。这样，还会为寻找正确的、一般性的解法提供有意义的启发。

④辅助解答

一道题目的完整解答，既有主要的实质性的步骤，也有次要的辅助性的步骤。实质性的步骤未找到之前，找辅助性的步骤是明智之举，既必不可少而又不困难。如：准确作图，把题目中的条件翻译成数学表达式，设应用题的未知数等。

书写也是辅助解答。"书写要工整、卷面能得分"是说第一印象好会在阅卷老师的心理上产生光环效应：书写认真—学习认真—成绩优良—给分偏高。

有些选择题，"大胆猜测"也是一种辅助解答，实际上猜测也是一种能力。

八、以快为上

高考数学试卷共有22个题，考试时间为两个小时，平均每题约为5.5分钟。为了给解答题的中高档题留下较充裕的时间，每道选择题、填空题应在一至二分钟之内解决。若这些题目用时太长，即使做对了也是"潜在丢分"，或"隐含失分"。一般，客观性试题与主观性试题的时间分配为4∶6。

九、立足中下题目，力争高水平

平时做作业，都是按所有题目来完成的，但高考却不然，只有个别的同学能交满分卷，因为时间和个别题目的难度都不允许多数学生去做完、做对全部题目，所以在答卷中要立足中下题目。中下题目通常占全卷的80%以上，是试题的主要构成，是考生得分的主要来源。学生能拿下这些题目，实际上就是数学科打了个胜仗，有了胜利在握的心理，对攻克高档题会更放得开。

十、立足一次成功，重视复查环节，不争交头卷

答卷中要做到稳扎稳打，字字有据，步步准确，尽量一次成功，提高成功率。试题做完后要认真做好解后检查，看是否有空题，答卷是否准确，所写字母与题中图形上的是否一致，格式是否规范，尤其是要审查字母、符号是否抄错。